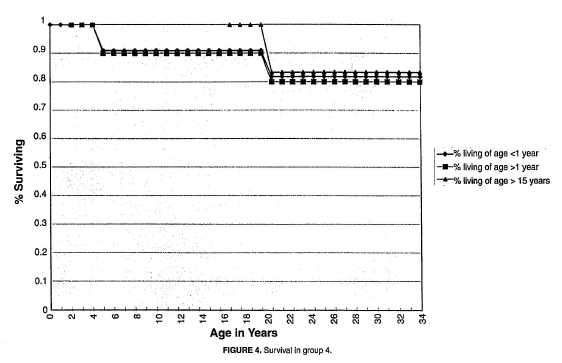
We now turn our attention to 1998 study by Plioplys et al.,1 and in particular to one of the many figures in the study: Figure 4. We choose to focus on this figure because the number of individuals involved in the analyses is small enough to make it very easy to see that something is wrong.
Figure 4 ostensibly illustrates the survival probabilities for group 4, defined in the study to be children who are: Fed by others, Not rolling, and have Hand or arm use present. In the figure there are three survival curves, one for children under a year of age, one for children above a year of age, and one for those above 15 years of age. We will focus on the curve for those under a year of age, which curve begins at age 0 and is marked with diamond-shaped markers. The figure in question is reproduced below.
We draw the following background information from the text of the study:
- Data were collected from 1986 to 1996, a period spanning 11 years at most (page 162, left column, end of first full paragraph).
- There were 11 persons meeting the criteria for group 4 (page 165, first paragraph).
Now we focus on Figure 4, and in particular on the survival curve for those in group 4 who were under a year of age. This curve, beginning at age 0 and marked with diamonds at each subsequent age, drops from 1 (or 100% survival) at age 4 to roughly 0.91 (91%) at age 5.
How could this figure of 91% have been calculated? There were at most 11 persons in group 4 who were under a year of age at the start of follow-up. If all 11 from group 4 were younger than 1 year of age, and if one of them died before or at 5 years of age, this would represent a survival probability of 10/11 = 91%. If fewer than 11 persons were alive in the “under age 1” group, or if more than one person died, there is no way this curve could drop to anything above 90%. (If the reader has any doubt about this, creating a simple table that considers all possibilities is simple enough. See here (pdf).) Thus we must conclude that all 11 persons in group 4 were alive prior to age 5 years during this study. In fact, since they were included in the analysis for the curve showing survival for the group who were “living of age < 1 year”, it is fair to assume that all 11 qualified for this criteria, i.e., all 11 were under a year of age sometime during this study. Further, since the study period spanned at most 11 years, these children who were under a year of age sometime during the study could have attained an age of at most 11 or 12 years during the study.
But wait! The survival curve for the “under a year of age” group begins at age 0 and goes all the way to age 34. If all 11 children were under a year of age at the start, and the study spanned only 11 years at most (from 1986 to 1996), there is no way this curve could continue to age 34. Something is terribly wrong.
Were the authors simply making up figures to illustrate in this graph? We don’t think so. In the final installment of this three part blog, we will explain what the authors likely did to end up with the erroneous figures in this, and in the many other graphs illustrated in their study. As we shall see, the mistake made is a classic example of what has been called the immortal time bias.2
Reference:
- Plioplys AV, Kasnicka I, Lewis S, Moller D. Survival rates among children with severe neurologic disabilities. South Med J. 1998 Feb;91(2):161-72.
- Shariff SZ, Cuerden MS, Jain AK, Garg AX. The secret of immortal time bias in epidemiologic studies. J Am Soc Nephrol. 2008 May;19(5):841-3.